At Hexham Middle School, we want our pupils to demonstrate perseverance in the face of mathematical problems and to develop their ability to communicate ideas using precise mathematical language and conventional notation. We seek to engender pupils with a sense of intrigue around the power of mathematics and we want our pupils to be curious to discover how key concepts interconnect and apply across the curriculum and in the wider world.

The mathematics curriculum has a focus on ensuring that pupils are fluent in numerical methods along with geometry, algebra, and statistics. Topics are interleaved across all years to consolidate learning and aid retention. Number skills are central to the curriculum and are practised regularly; this is in recognition of the fact that barriers with number fluency can result in cognitive overload when pupils attempt to learn new material at a later point, such as topics in geometry which rely heavily on numerical fluency. Pupils who already demonstrate a secure fluency or who grasp concepts rapidly will be encouraged to apply their understanding to deeper and mathematically richer problems. We understand pupils learn at different speeds and we fully embrace adaptive teaching to support and challenge pupils appropriately throughout the curriculum.

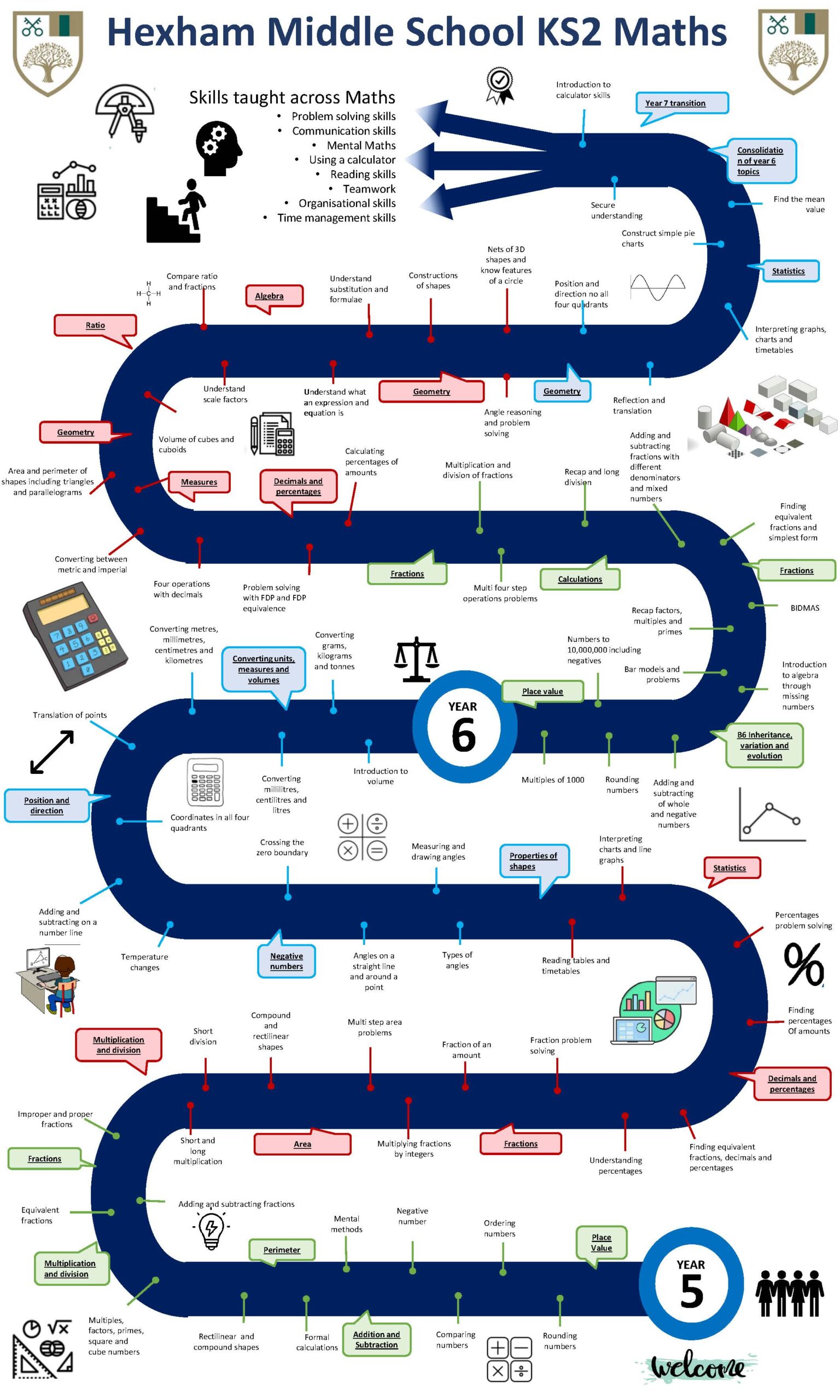
The Year 5 curriculum begins with place value and number skills to secure pupils understanding from Year 4. The key skills in the Autumn term include four operations, perimeter, understanding of numbers such as primes, multiples, factors, square and cube numbers and then fractions. This is followed in the spring term by further fraction work which links to percentages and decimals and the perimeter work will build up to area. In the Summer term students are introduced to properties of shapes along with negative numbers, converting measures and directions.  All the skills learnt in Year 5 extend the foundations from years 3 and 4. It is crucial pupils are fluent with arithmetic skills and can apply their mathematical thinking to reasoning questions.

In year 6 we build upon the work in year 5 and start the year with a recap and deepening of place value, calculations and multiplying and dividing with fractions.  This allows students to familiarise themselves with the number skills required for the year and deepen their understanding where applicable. In the spring term we introduce some new concepts such as volume, ratio, properties of 3d shapes and algebra. This is on top of reviewing and extending pupils knowledge in perimeter, area, decimals, and percentages. In the summer term we focus on statistics and some more geometry whilst consolidating number skills. The summer term is also key for year 6 pupils as they will complete their SATs assessment. All the skills covered at Key stage 2 are built upon at Key stage 3 and 4 and the foundations learnt in year 6 will support learning all the way up to GCSE.

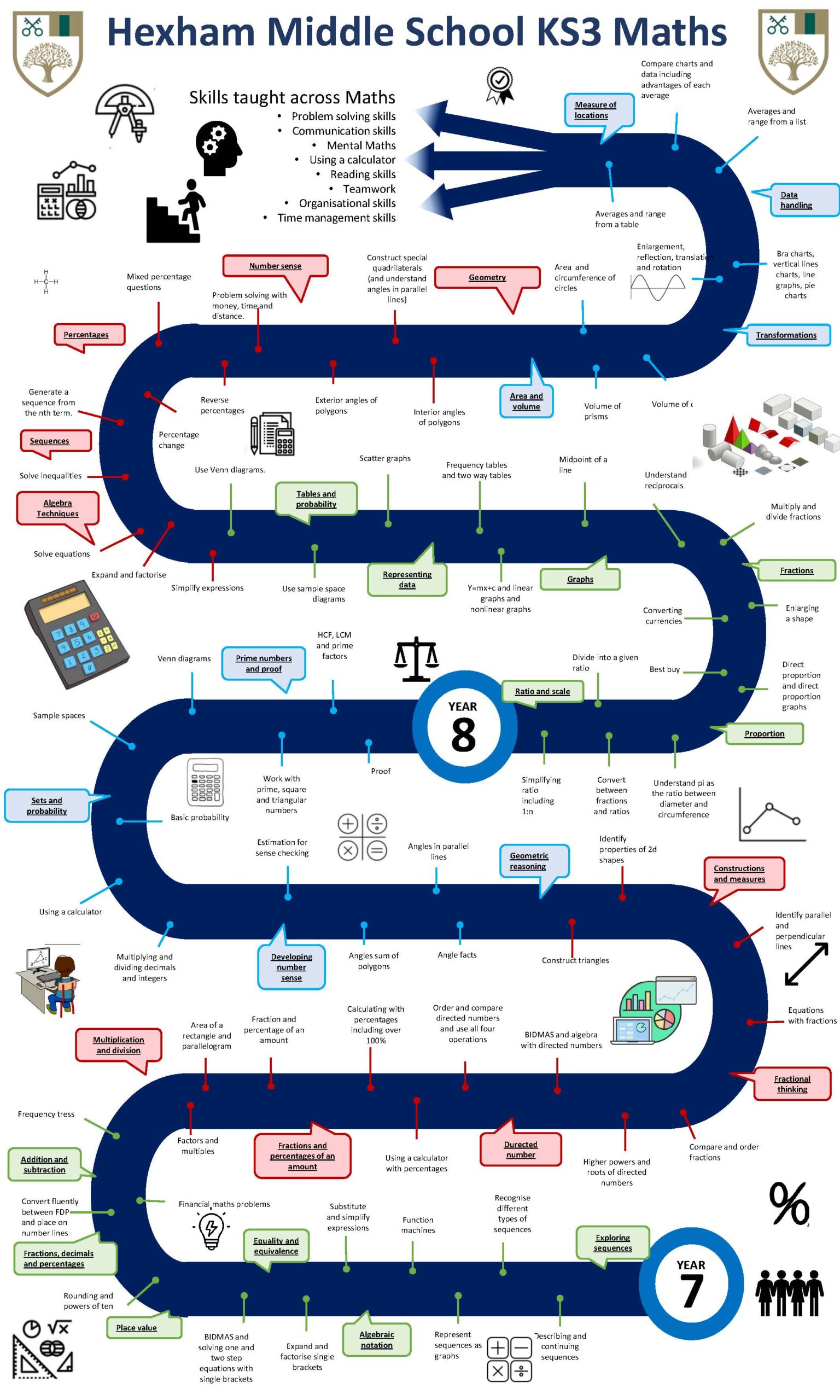
The Year 7 curriculum begins with algebraic thinking to introduce the children to Key Stage 3 with new content. They will learn about sequences and develop their understanding of algebraic notation and manipulation. This is to allow them to apply this in future topics and develop their problem-solving skills. Algebra is then interleaved throughout as we move onto place value, proportion and fraction, decimal and percentage equivalence which are covered in order to consolidate and extend the foundations from Key Stage 2. Throughout the spring term, the curriculum focuses on solving complex problems and deepening mathematical thinking. This is followed by a focus on directed number and further developing fluency with fractions in response to the demands of the high school curriculum. The summer term covers geometric reasoning which draws out the ability to articulate mathematical thinking whilst applying number skills, and finally introduces the students to basic concepts of probability. The need for reasoning, justifications and proof is woven throughout our topic blocks, however, an explicit unit on proof is included to allow students to explore the language and skills involved in providing a mathematical proof.

In Year 8, the curriculum begins with proportional reasoning in order to prepare the pupils for the increased focus on this area in the high school curriculum. Pupils are introduced to graphical representation which links to the work on proportion and builds on the algebraic work covered in Year 7. These topics allow pupils to recognise the links between sequences, linear graphs and representations of data as well as finding the nth term of sequences. The spring term further develops our pupils’ use of number and proportion before moving onto angles, area and volume. These topics provide an excellent opportunity to develop pupils’ algebraic understanding. In the summer term, they will revisit algebra to ensure that the key concepts met so far are secure, and if so, are developed further, in preparation for year 9 and beyond. The year ends with a statistics focus in which pupils develop their understanding of dispersion and location: this will prepare them for real life application of mathematics.

At QEHS, Year 9 builds upon the work undertaken in Years 7 and 8 and is assured through the close Partnership working around the mathematics curriculum intentions. During the autumn term, students work on consolidating and developing their skills in place value, fractions, decimals, percentages, ratio and proportion at the appropriate level. Towards the end of the first term, probability is introduced to connect and apply the learning around fractions and decimals in particular. As the year progresses, students are introduced to algebraic methods, connecting back to earlier number topics and which again, provide a solid foundation for later study of new topics in algebra, geometry and measures and statistics. We recognise the importance of giving students the skills to reason mathematically and to apply their knowledge to problems, once they are fluent in mathematical methods. As such, every lesson in Year 9 incorporates an opportunity for the teacher to model and/or for students to apply reasoning and problem-solving skills, thereby contextualising and applying mathematical methods in a variety of settings. Across the Hexham Partnership of Schools, we have worked collaboratively to develop a consistent ‘Calculation Policy’ (see below).